Arrays
NumPy is a widely-used Python library for numerical computing that provides
efficient data structures for working with arrays and matrices, as well as a
large collection of mathematical functions for operations such as linear
algebra, Fourier analysis, and random number generation. It is the defacto
standard array container within Python, but unlike many other array containers
it can also explicitly represent multidimensional arrays, and has powerful
broadcasting rules for performing operations on arrays with different
numbers of dimensions.
Adding NumPy to our Virtual Environment
In order to use NumPy we first need to install it using
pip (it is not part of
the standard Python library). First ensure that you are working in a virtual
environment, either a new one or an existing environment that you would like to
install NumPy in.For example, say we wish to create a new "learning numpy" project, and create a new environment within this project. We can type the following:
mkdir learning_numpy cd learning_numpy python3 -m venv venv source venv/bin/activate
Then we can use
pip to install numpy:pip install numpy
This reflects a typical way of working with virtual environments: a new project
comes along, we create a new virtual environment in a location close to where
we're working (typically in the same directory as our code), we activate that
virtual environment and install the packages we'll need for the work.
NumPy Arrays vs Python Lists
NumPy's array type represents a multidimensional array or tensor Mi,j,k...n
The NumPy array seems at first to be just like a list:
import numpy as np my_array = np.array(range(5)) my_array
Note here we are importing the NumPy module as
np, an established convention
for using NumPy which means we can refer to NumPy using np. instead of the
slightly more laborious numpy..array([0, 1, 2, 3, 4])
Ok, so they look like a list.
my_array[2]
2
We can access them like a list.
We can also access NumPy arrays as a collection in
for loops:for element in my_array: print("Hello" * element)
Hello HelloHello HelloHelloHello HelloHelloHelloHello
However, we can also see our first weakness of NumPy arrays versus Python lists:
my_array.append(4)
Traceback (most recent call last): File "<stdin>", line 1, in <module> AttributeError: 'numpy.ndarray' object has no attribute 'append'
For NumPy arrays, you typically don't change the data size once you've defined
your array, whereas for Python lists, you can do this efficiently. Also, NumPy
arrays only contain one datatype. However, you get back lots of goodies in
return...
Elementwise Operations
One great advantage of NumPy arrays is that most operations can be applied element-wise automatically, and in a very Pythonic way!
my_array + 2
+ in this context is an elementwise operation performed on all the matrix elements, and gives us:array([2, 3, 4, 5, 6])
Other elementwise operations
Try using
-, *, / in the above statement instead. Do they do what you expect?These are known as 'vectorised' operations, and are very fast.
But for now, let's take a brief look at a basic example that demonstrates the
performance of NumPy over Python lists. First, using Python lists we can do the
following, that creates a 2D list of size 10000x10000, sets all elements to
zero, then adds 10 to all those elements:
nested_list = [[0 for _ in range(10000)] for _ in range(10000)] nested_list = [[x+10 for x in column] for column in nested_list]
That took a while! In NumPy we replicate this by doing:
import numpy as np array = np.zeros((10000, 10000)) array = array + 10
Here, we import the NumPy library, use a specialised function to set up a NumPy
array of size 5000x5000 with elements set to zero, and then - in a very Pythonic
way - add 10 to each element. It's simpler, closer to our conceptual model of
what we want to achieve, and due to NumPy's optimisations for dealing with
matrices, it's much faster.
Introducing an Inflammation Dataset
We're now going to use an example dataset based on a clinical trial of
inflammation in patients who have been given a new treatment for arthritis.
Let's download this dataset now. First, create a new directory inflammation and
cd to it:mkdir inflammation cd inflammation
If on WSL or Linux (e.g. Ubuntu or the Ubuntu VM), then do:
wget https://www.uhpc-training.co.uk/material/HPCu/software_architecture_and_design/procedural/inflammation/inflammation.zip
Or, if on a Mac, do:
curl -O https://www.uhpc-training.co.uk/material/HPCu/software_architecture_and_design/procedural/inflammation/inflammation.zip
Once done, you can unzip this file using the
unzip command in Bash, which will unpack all the files
in this zip archive into the current directory:unzip inflammation.zip
This zip file contains some code as well as the datasets we need stored in the
data directory (which is what we're
interested in).cd data
What Does the Patient Inflammation Data Contain?
Each dataset records inflammation measurements from a separate clinical trial of the drug, and each dataset contains information for 60 patients, who had their inflammation levels recorded for 40 days whilst participating in the trial.
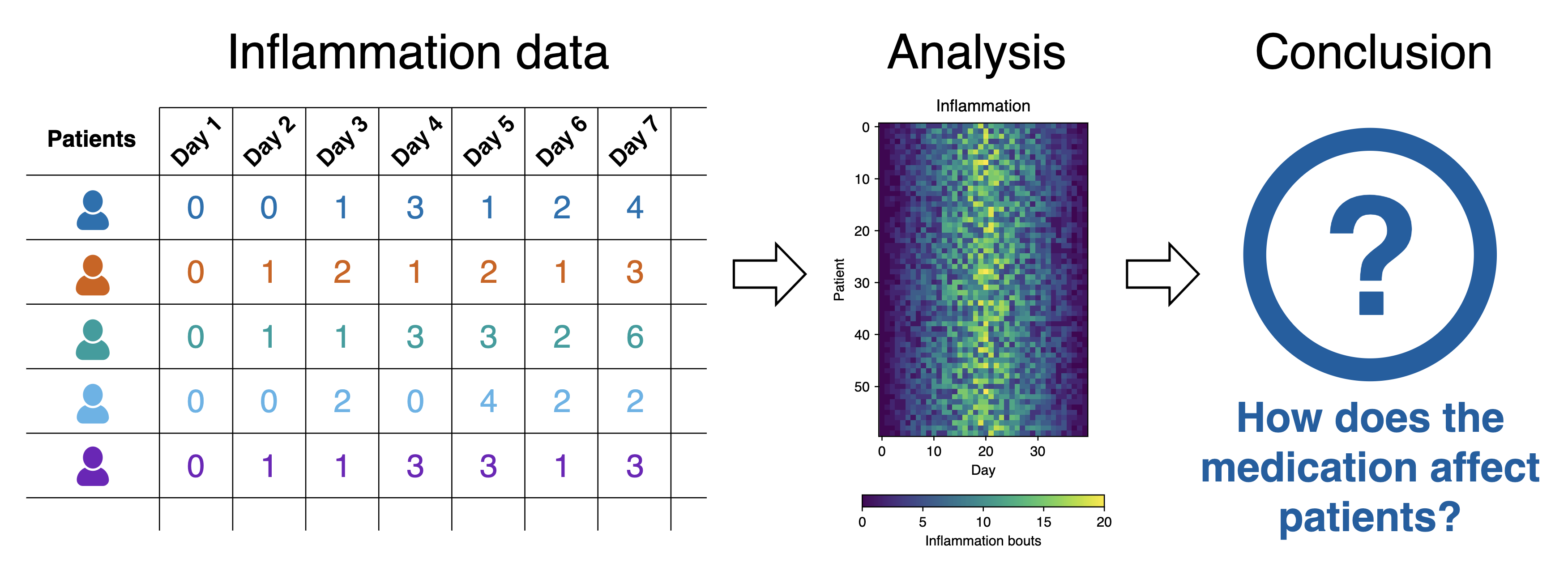Inflammation study pipeline from the Software Carpentry Python novice lesson
Each of the data files uses the popular comma-separated (CSV) format to represent the data, where:
- Each row holds inflammation measurements for a single patient,
- Each column represents a successive day in the trial,
- Each cell represents an inflammation reading on a given day for a patient (in some arbitrary units of inflammation measurement).
We can use first NumPy to load our dataset into a Python variable:
data = np.loadtxt(fname='../data/inflammation-01.csv', delimiter=',') data
array([[0., 0., 1., ..., 3., 0., 0.], [0., 1., 2., ..., 1., 0., 1.], [0., 1., 1., ..., 2., 1., 1.], ..., [0., 1., 1., ..., 1., 1., 1.], [0., 0., 0., ..., 0., 2., 0.], [0., 0., 1., ..., 1., 1., 0.]])
So, the data in this case has 60 rows (one for each patient) and 40 columns (one for each day) as we would expect. Each cell in the data represents an inflammation reading on a given day for a patient. So this shows the results of measuring the inflammation of 60 patients over a 40 day period.
In the Corner
What may also surprise you is that when Python displays an array,
it shows the element with index
[0, 0] in the upper left corner
rather than the lower left.
This is consistent with the way mathematicians draw matrices
but different from the Cartesian coordinates.
The indices are (row, column) instead of (column, row) for the same reason,
which can be confusing when plotting data.Examining our Dataset
Let's ask what type of thing
data refers to:print(type(data))
<class 'numpy.ndarray'>
The output tells us that
data currently refers to an N-dimensional array, the functionality for which is provided by the NumPy library.Data Type
A Numpy array contains one or more elements of the same type. The
type function will only tell you that a variable is a NumPy array but won't tell you the type of thing inside the array. We can find out the type of the data contained in the NumPy array.print(data.dtype)
float64
This tells us that the NumPy array's elements are 64-bit floating-point numbers.
With the following command, we can see the array's shape:
print(data.shape)
(60, 40)
The output tells us that the
data array variable contains 60 rows and 40 columns, as we would expect.We can also access specific elements of our 2D array (such as the first value) like this:
data[0, 0]
0.0
Or the value in the middle of the dataset:
data[30, 20]
13.0
Slicing our Inflammation Data
An index like
[30, 20] selects a single element of an array, but similar to how we slice lists, we can slice whole sections of NumPy arrays as well.For example, we can select the first ten days (columns) of values for the first four patients (rows) like this:
data[0:4, 0:10]
array([[0., 0., 1., 3., 1., 2., 4., 7., 8., 3.], [0., 1., 2., 1., 2., 1., 3., 2., 2., 6.], [0., 1., 1., 3., 3., 2., 6., 2., 5., 9.], [0., 0., 2., 0., 4., 2., 2., 1., 6., 7.]])
So here
0:4 means, "Start at index 0 and go up to, but not including, index
4." Again, the up-to-but-not-including takes a bit of getting used to, but the
rule is that the difference between the upper and lower bounds is the number of
values in the slice.And as we saw with lists, we don't have to start slices at 0:
data[5:10, 0:10]
Which will show us data from patients 5-9 (rows) across the first 10 days (columns):
array([[0., 0., 1., 2., 2., 4., 2., 1., 6., 4.], [0., 0., 2., 2., 4., 2., 2., 5., 5., 8.], [0., 0., 1., 2., 3., 1., 2., 3., 5., 3.], [0., 0., 0., 3., 1., 5., 6., 5., 5., 8.], [0., 1., 1., 2., 1., 3., 5., 3., 5., 8.]])
We also don't have to include the upper and lower bound on the slice. If we don't include the lower bound, Python uses 0 by default; if we don't include the upper, the slice runs to the end of the axis, and if we don't include either (i.e., if we just use ':' on its own), the slice includes everything:
small = data[:3, 36:] small
The above example selects rows 0 through 2 and columns 36 through to the end of the array:
array([[2., 3., 0., 0.], [1., 1., 0., 1.], [2., 2., 1., 1.]])
Numpy Memory
Numpy memory management can be tricksy:
x = np.arange(5) y = x[:]
y[2] = 0 x
array([0, 1, 0, 3, 4])
It does not behave like lists!
x = list(range(5)) y = x[:]
y[2] = 0 x
[0, 1, 2, 3, 4]
We can use
np.copy() to force the use of separate memory and actually copy the
values. Otherwise NumPy tries its hardest to make slices be views on data,
referencing existing values and not copying them. So an example using
np.copy():x = np.arange(5) y = np.copy(x) y[2] = 0 x
array([0, 1, 2, 3, 4])
Elementwise Operations on Multiple Arrays
As we've seen, arrays also know how to perform common mathematical operations on their values element-by-element:
doubledata = data * 2.0
Will create a new array
doubledata, each element of which is twice the value of the corresponding element in data:print('original:') data[:3, 36:] print('doubledata:') doubledata[:3, 36:]
original: array([[2., 3., 0., 0.], [1., 1., 0., 1.], [2., 2., 1., 1.]]) doubledata: array([[4., 6., 0., 0.], [2., 2., 0., 2.], [4., 4., 2., 2.]])
If, instead of taking an array and doing arithmetic with a single value (as
above), you did the arithmetic operation with another array of the same shape,
the operation will be done on corresponding elements of the two arrays:
tripledata = doubledata + data
Will give you an array where
tripledata[0,0] will equal doubledata[0,0] plus data[0,0],
and so on for all other elements of the arrays.print('tripledata:') print(tripledata[:3, 36:])
tripledata: array([[6., 9., 0., 0.], [3., 3., 0., 3.], [6., 6., 3., 3.]])
Stacking Arrays
Arrays can be concatenated and stacked on top of one another,
using NumPy's
vstack and hstack functions for vertical and horizontal stacking, respectively.import numpy as np A = np.array([[1,2,3], [4,5,6], [7,8,9]]) print('A = ') print(A) B = np.hstack([A, A]) print('B = ') print(B) C = np.vstack([A, A]) print('C = ') print(C)
A = [[1 2 3] [4 5 6] [7 8 9]] B = [[1 2 3 1 2 3] [4 5 6 4 5 6] [7 8 9 7 8 9]] C = [[1 2 3] [4 5 6] [7 8 9] [1 2 3] [4 5 6] [7 8 9]]
Write some additional code that slices the first and last columns of our inflammation
data array,
and stacks them into a 60x2 array, to give us data from the first and last days of our trial across all patients.
Make sure to print the results to verify your solution.Dot Products
You can also do dot products of NumPy arrays:
a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) np.dot(a, b)
array([[19, 22], [43, 50]])
More Complex Operations
Often, we want to do more than add, subtract, multiply, and divide array elements. NumPy knows how to do more complex operations, too. If we want to find the average inflammation for all patients on all days, for example, we can ask NumPy to compute
data's mean value:print(np.mean(data))
6.14875
mean is a function that takes an array as an argument.Not All Functions Have Input
Generally, a function uses inputs to produce outputs.
However, some functions produce outputs without
needing any input. For example, checking the current time
doesn't require any input.
import time print(time.ctime())
{: .language-python}
Fri Sep 30 14:52:40 2022
{: .output}
For functions that don't take in any arguments,
we still need parentheses (
())
to tell Python to go and do something for us.NumPy has lots of useful functions that take an array as input.
Let's use three of those functions to get some descriptive values about the
dataset. We'll also use multiple assignment, a convenient Python feature that
will enable us to do this all in one line.
maxval, minval, stdval = np.max(data), np.min(data), np.std(data) print('max inflammation:', maxval) print('min inflammation:', minval) print('std deviation:', stdval)
Here we've assigned the return value from
np.max(data) to the variable maxval, the value
from np.min(data) to minval, and so on.max inflammation: 20.0 min inflammation: 0.0 std deviation: 4.613833197118566
When analyzing data, though, we often want to look at variations in statistical values, such as the maximum inflammation per patient or the average inflammation per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:
np.max(data[0, :])
So here, we're looking at the maximum inflammation across all days for the first patient, which is
18.0
What if we need the maximum inflammation for each patient over all days (as in
the next diagram on the left) or the average for each day (as in the diagram on
the right)? As the diagram below shows, we want to perform the operation across
an axis:
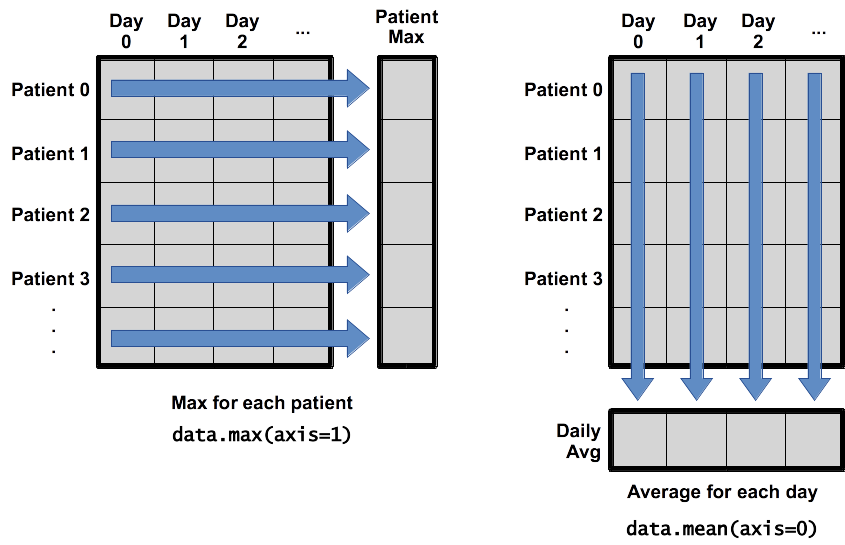
To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
print(np.mean(data, axis=0))
[ 0. 0.45 1.11666667 1.75 2.43333333 3.15 3.8 3.88333333 5.23333333 5.51666667 5.95 5.9 8.35 7.73333333 8.36666667 9.5 9.58333333 10.63333333 11.56666667 12.35 13.25 11.96666667 11.03333333 10.16666667 10. 8.66666667 9.15 7.25 7.33333333 6.58333333 6.06666667 5.95 5.11666667 3.6 3.3 3.56666667 2.48333333 1.5 1.13333333 0.56666667]
As a quick check, we can ask this array what its shape is:
print(np.mean(data, axis=0).shape)
(40,)
The expression
(40,) tells us we have an N×1 vector, so this is the average
inflammation per day for all patients. If we average across axis 1 (columns in
our 2D example), we get:patients_avg = np.mean(data, axis=1) patients_avg
[ 5.45 5.425 6.1 5.9 5.55 6.225 5.975 6.65 6.625 6.525 6.775 5.8 6.225 5.75 5.225 6.3 6.55 5.7 5.85 6.55 5.775 5.825 6.175 6.1 5.8 6.425 6.05 6.025 6.175 6.55 6.175 6.35 6.725 6.125 7.075 5.725 5.925 6.15 6.075 5.75 5.975 5.725 6.3 5.9 6.75 5.925 7.225 6.15 5.95 6.275 5.7 6.1 6.825 5.975 6.725 5.7 6.25 6.4 7.05 5.9 ]
Which is the average inflammation per patient across all days.
Change in Inflammation
This patient data is longitudinal in the sense that each row represents a
series of observations relating to one individual. This means that
the change in inflammation over time is a meaningful concept.
The
np.diff() function takes a NumPy array and returns the
differences between two successive values along a specified axis. For
example, a NumPy array that looks like this:npdiff = np.array([ 0, 2, 5, 9, 14])
Calling
np.diff(npdiff) would do the following calculations and
put the answers in another array.[ 2 - 0, 5 - 2, 9 - 5, 14 - 9 ]
np.diff(npdiff)
array([2, 3, 4, 5])
Which axis would it make sense to use this function along?
If the shape of an individual data file is
(60, 40) (60 rows and 40
columns), what would the shape of the array be after you run the diff()
function and why?How would you find the largest change in inflammation for each patient? Does
it matter if the change in inflammation is an increase or a decrease?
Broadcasting
This is another really powerful feature of NumPy, and covers a 'special case' of array multiplication.
By default, array operations are element-by-element:
np.arange(5) * np.arange(5)
array([ 0, 1, 4, 9, 16])
If we multiply arrays with non-matching shapes we get an error:
np.arange(5) * np.arange(6)
Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: operands could not be broadcast together with shapes (5,) (6,)
Or with a multi-dimensional array:
np.zeros([2,3]) * np.zeros([2,4])
Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: operands could not be broadcast together with shapes (2,3) (2,4)
Arrays must match in all dimensions in order to be compatible:
np.ones([3, 3]) * np.ones([3, 3]) # Note elementwise multiply, *not* matrix multiply.
array([[ 1., 1., 1.], [ 1., 1., 1.], [ 1., 1., 1.]])
Except, that if one array has any Dimension size of 1, then the data is
automatically REPEATED to match the other dimension. This is known as
**broadcasting.
So, let's consider a subset of our inflammation data (just so we can easily see
what's going on):
subset = data[:10, :10] subset
array([[0., 0., 1., 3., 1., 2., 4., 7., 8., 3.], [0., 1., 2., 1., 2., 1., 3., 2., 2., 6.], [0., 1., 1., 3., 3., 2., 6., 2., 5., 9.], [0., 0., 2., 0., 4., 2., 2., 1., 6., 7.], [0., 1., 1., 3., 3., 1., 3., 5., 2., 4.], [0., 0., 1., 2., 2., 4., 2., 1., 6., 4.], [0., 0., 2., 2., 4., 2., 2., 5., 5., 8.], [0., 0., 1., 2., 3., 1., 2., 3., 5., 3.], [0., 0., 0., 3., 1., 5., 6., 5., 5., 8.], [0., 1., 1., 2., 1., 3., 5., 3., 5., 8.]])
Let's assume we wanted to multiply each of the 10 individual day values in a
patient row for every patient, by contents of the following array:
multiplier = np.arange(1, 11) multiplier
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
So, the first day value in a patient row is multiplied by 1, the second day by 2, the third day by 3, etc.
We can just do:
subset * multiplier
array([[ 0., 0., 3., 12., 5., 12., 28., 56., 72., 30.], [ 0., 2., 6., 4., 10., 6., 21., 16., 18., 60.], [ 0., 2., 3., 12., 15., 12., 42., 16., 45., 90.], [ 0., 0., 6., 0., 20., 12., 14., 8., 54., 70.], [ 0., 2., 3., 12., 15., 6., 21., 40., 18., 40.], [ 0., 0., 3., 8., 10., 24., 14., 8., 54., 40.], [ 0., 0., 6., 8., 20., 12., 14., 40., 45., 80.], [ 0., 0., 3., 8., 15., 6., 14., 24., 45., 30.], [ 0., 0., 0., 12., 5., 30., 42., 40., 45., 80.], [ 0., 2., 3., 8., 5., 18., 35., 24., 45., 80.]])
Which gives us what we want, since each value in
multiplier is applied
successively to each value in a patient's row, but over every patient's row. So,
every patient's first value is multiplied by 1, every patient's second value is
multiplied by 2, etc.Since
multiplier has only one dimension, but the size of that dimension
matches our number of days (the second dimension of subset), broadcasting
automatically repeats the data in multiplier to match the number of patients
(the first dimension in subset) so the * operation can be applied over
arrays of equal shape.Key Points
- Processing NumPy arrays is generally much faster than processing Python lists.
- NumPy arrays have specialised capabilities to support complex mathematical operations, and are less flexible that Python lists.
- Slicing NumPy arrays returns a reference to the original dataset, not a copy of it like with Python lists.
- NumPy arrays only hold elements of a single data type and are generally fixed in size.
- Use
numpy.mean(array),numpy.max(array), andnumpy.min(array)to calculate simple statistics. - Use
numpy.mean(array, axis=0)ornumpy.mean(array, axis=1)to calculate statistics across the specified axis. - Broadcasting allows you to apply an operation to two arrays of different shape, repeating the data in an array of a one-long dimension to match the larger array.